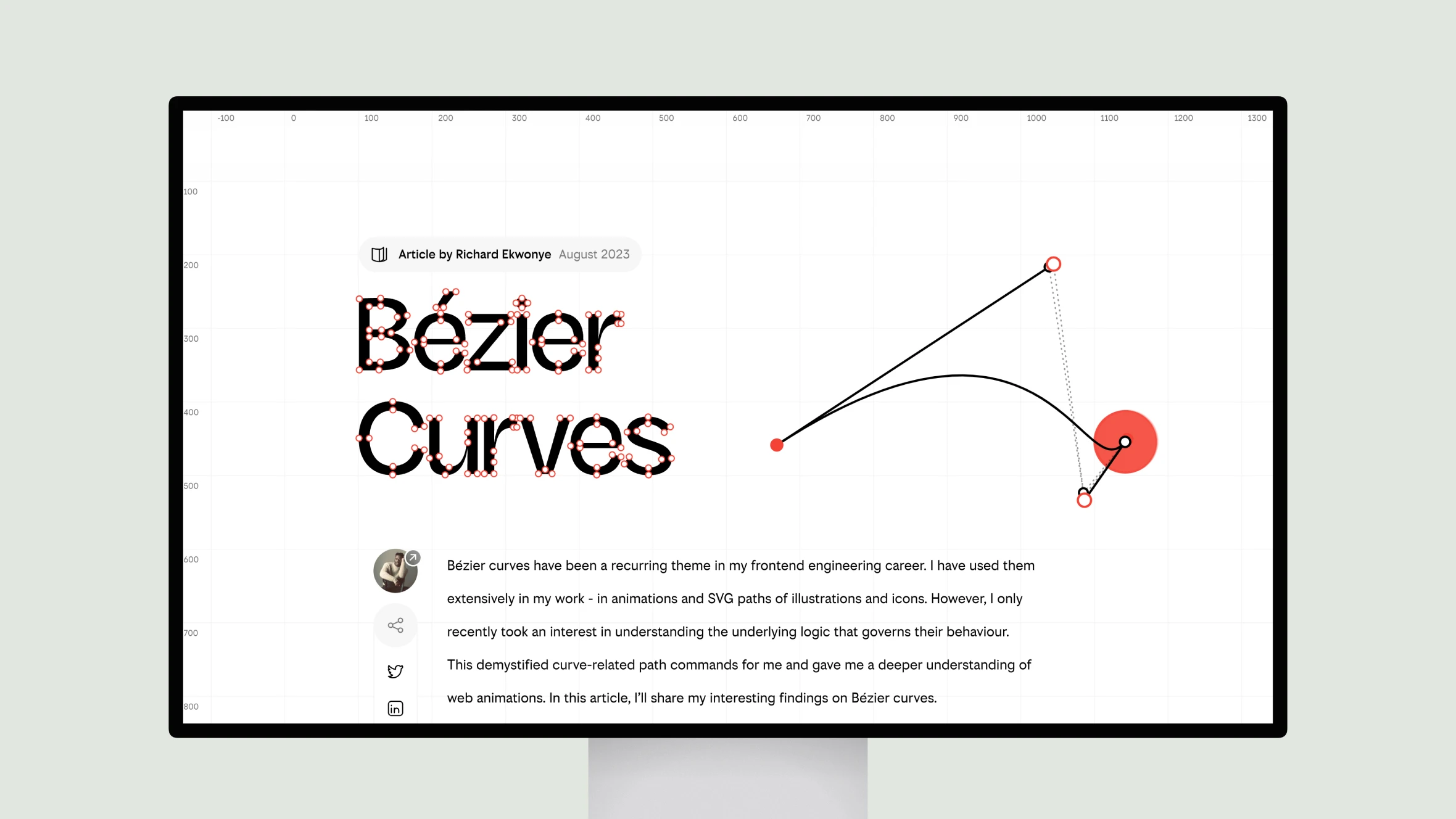
The article discusses Bézier curves, which are mathematical formulas used to generate smooth curved paths for graphics, animations and designs. It explores the underlying logic and algorithms that govern how Bézier curves behave.
The author shares their journey of deepening their understanding of Bézier curves, from using them extensively in frontend work to researching how they are derived. Key topics covered include cubic Bézier easing functions in CSS animations, the use of quadratic and cubic Bézier curves in SVG paths, and De Casteljau’s algorithm for obtaining points along a Bézier curve.
Interactive examples and visualizations are provided to illustrate Bézier curves and easing functions. The article aims to build knowledge of this important graphics concept and inspire readers to apply their newfound skills in creative projects.